Sinüs Teoremi Nedir?Sinüs Teoremi, geometri alanında önemli bir yere sahip olan bir teoremdir. Özellikle üçgenlerin kenar uzunlukları ve açıları arasındaki ilişkiyi tanımlar. Bu teorem, herhangi bir üçgenin kenar uzunlukları ile karşılık gelen açıların sinüs değerleri arasındaki orantıyı ifade eder. Sinüs Teoremi, üçgenlerin çözümünde, alan hesaplamalarında ve çeşitli mühendislik uygulamalarında sıkça kullanılır. Sinüs Teoreminin FormülüSinüs Teoremi, aşağıdaki formül ile ifade edilir:
Burada;- a, A açısının karşısındaki kenar uzunluğudur.- b, B açısının karşısındaki kenar uzunluğudur.- c, C açısının karşısındaki kenar uzunluğudur.- A, B ve C, üçgenin iç açılarının ölçüleridir. Sinüs Teoreminin UygulamalarıSinüs Teoremi, birçok alanda geniş bir uygulama yelpazesine sahiptir. Bu uygulamalardan bazıları şunlardır:
Sinüs Teoreminin KanıtıSinüs Teoreminin kanıtı, çeşitli yöntemlerle gerçekleştirilebilir. En yaygın kanıtlardan biri, üçgenin yüksekliğini kullanarak yapılan kanıttır. Bu kanıtın ana hatları şu şekildedir: 1. Üçgenin bir kenarının üzerine dik bir yükseklik çizilir.2. Yüksekliğin, üçgenin alanını iki farklı şekilde hesaplamak için kullanılabileceği gösterilir.3. Her iki alan ifadesi eşit olduğu için, sinüs değerleri arasında bir ilişki elde edilir. Bu adımlar sonucunda, sinüs teoreminin geçerliliği kanıtlanmış olur. Sinüs Teoremi ile İlgili Ekstra Bilgiler |
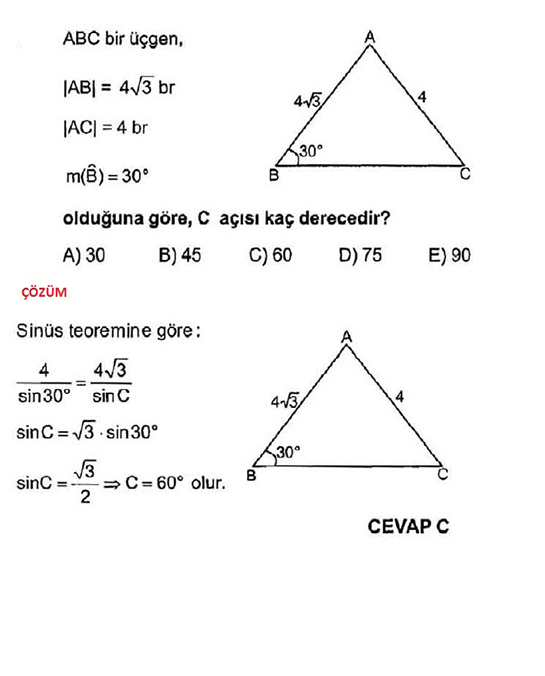
Sinüs teoremi hakkında bilgi edinirken, sinüs 30 kaçtır sorusunu duymak oldukça yaygındır. Sinüs 30, matematikte önemli bir değerdir ve 0.5 olarak bilinir. Bu değer, üçgenlerin kenar uzunluklarını ve açılarını anlamamıza yardımcı olur.
Cevap yazSinüs Teoremi ve Sinüs 30 hakkında verdiğiniz bilgiler oldukça değerli, Rastkâr. Sinüs teoremi, bir üçgende kenar uzunlukları ile karşıt açıların sinüsleri arasındaki ilişkiyi ortaya koyar. Sinüs 30'un 0.5 değeri, özellikle 30 derece açısına sahip üçgenlerde, üçgenin kenar uzunluklarını hesaplamak için oldukça kullanışlıdır.
Matematiksel Önemi açısından, sinüs değerleri trigonometrik hesaplamalarda sıkça kullanılır. Sinüs 30'un değeri, bir kenarın uzunluğunun yarısına eşit olan bir karşı kenar ile bağlantılıdır. Bu durum, geometrik problemlerde ve inşaat mühendisliğinde sıklıkla karşılaşılan bir durumdur.
Uygulama Alanları da oldukça geniştir. Sinüs teoremi, mühendislik, fizik ve mimarlık gibi alanlarda üçgenler arası ilişkilere dayalı birçok hesaplamanın temelini oluşturur. Sinüs 30'un bilinmesi, bu alanlarda çalışanlar için önemli bir avantaj sağlar.
Sonuç olarak, sinüs değerleri ve özellikle sinüs 30, matematiksel problemlerin çözümünde ve teorik uygulamalarda vazgeçilmez bir rol oynamaktadır.
Sinüs teoremi formülü, üçgenlerin kenarları ve açıları arasındaki ilişkiyi anlamak için çok önemli. Bu formül sayesinde, herhangi bir üçgende kenarların sinüslerinin oranlarını kullanarak, bilinmeyen kenar veya açıları kolayca bulabiliyoruz. Gerçekten de matematiğin temel taşlarından biri!
Cevap yazSinüs Teoremi Nedir?
Oğuzer, sinüs teoremi, bir üçgende kenar uzunlukları ile karşısındaki açıların sinüslerinin oranlarını belirten önemli bir matematik kuralıdır. Bu teorem, herhangi bir üçgende, kenarların uzunlukları ile açıların sinüsleri arasında belirli bir ilişki kurarak, bilinmeyen kenar veya açıları bulmamıza olanak tanır.
Uygulama Alanları
Sinüs teoremi, geometrik problemlerin yanı sıra fiziksel uygulamalarda da sıklıkla kullanılır. Özellikle, mühendislik ve mimarlık gibi alanlarda, üçgenlerin boyutları ile ilgili hesaplamalarda büyük kolaylık sağlar. Bu sayede karmaşık üçgen yapılarının analizi daha basit hale gelir.
Matematiksel Önemi
Matematiğin temel taşlarından biri olarak kabul edilen sinüs teoremi, özellikle trigonometri alanında önemli bir yere sahiptir. Bu teoremi anlamak, daha karmaşık matematiksel kavramları öğrenmek için de bir temel oluşturur. Oğuzer, bu nedenle sinüs teoremini öğrenmek ve uygulamak, matematiksel düşünme becerimizi geliştirmek açısından büyük önem taşır.
Sinüs teoremi, üçgenlerdeki kenar ve açılar arasındaki ilişkiyi gösterir. Sinüs alan formülü ise bir üçgenin alanını bulmak için kullanılır: Alan = 0.5 a b sin(C). Bu formül, üçgenlerin alan hesaplamasında büyük kolaylık sağlar.
Cevap yazSinüs Teoremi ve Alan Formülü
Taze, Sinüs teoremi, üçgenlerde kenar ve açıların ilişkisini anlamak için gerçekten çok önemli bir araçtır. Üçgenlerdeki açıların ve karşı kenarların oranlarını kullanarak, bilinmeyen kenarları veya açıları bulmamıza yardımcı olur. Sinüs alan formülü de aynı şekilde, özellikle üçgenin iki kenarı ve aralarındaki açı verildiğinde, alan hesaplamasını oldukça kolaylaştırır.
Bu formül, yalnızca üçgenlerin alanını hesaplamakla kalmaz, aynı zamanda trigonometrik ilişkilerin pratikte nasıl kullanılabileceğini de gösterir. Özellikle geometri ve trigonometri derslerinde, bu tür formüllerin öğrenilmesi, daha karmaşık matematiksel problemleri çözmek için temel bir beceri haline gelir. Sinüs teoremini ve alan formülünü iyi anlamak, ilerleyen konularda başarılı olmanıza büyük katkı sağlayacaktır.
Kosinüs teoremi fizik açısından da oldukça önemli bir yere sahip. Özellikle kuvvetlerin bileşkesini hesaplarken, açıların ve kenar uzunluklarının ilişkisini belirlemek için kullanıyoruz. Bu sayede, çokgen sistemlerde hareket analizlerini daha kolay yapabiliyoruz. Kosinüs teoremi fizik derslerinde sıkça karşımıza çıkıyor.
Cevap yazKosinüs Teoremi ve Önemi
Raci, kosinüs teoreminin fizik açısından önemi gerçekten büyüktür. Kuvvetlerin bileşkesini hesaplarken, bu teoremi kullanmak, karmaşık durumları daha anlaşılır hale getirir. Özellikle çokgen sistemlerde, kuvvetlerin yönleri ve büyüklükleri arasındaki ilişkiyi net bir şekilde belirleyebilmemiz, hareket analizlerini kolaylaştırır. Bu sayede, fizik derslerinde karşılaştığımız birçok problem daha basit bir şekilde çözüme kavuşturulabilir. Kosinüs teoreminin bu tür uygulamaları, fiziksel olayların daha iyi anlaşılmasına katkı sağlıyor.
Sinüs teoremi hakkındaki bu bilgileri okuduktan sonra, sin(A)=a/2R formülünü nasıl kullanacağım konusunda biraz karıştım. Bu formülü bir örnekle açıklayabilir misiniz? Ayrıca, çevrel çemberin yarıçapını bulmanın pratik bir yolu var mı?
Cevap yazMerhaba Haccac,
Sinüs Teoremi ve Formülün Kullanımı
Sinüs teoremi, bir üçgende karşı kenar uzunluklarının sinüs değerleri ile orantılı olduğunu belirtir. Sin(A) = a / 2R formülü, burada a karşı kenar uzunluğunu, A açısını ve R ise çevrel çemberin yarıçapını temsil eder. Örneğin, bir üçgende A açısı 30° ve karşısındaki kenar a = 6 birim ise:
Sin(30°) = 0.5 olduğu için, formülü kullanarak R’yi bulabiliriz.
0.5 = 6 / (2R)
Buradan 2R = 6 / 0.5 = 12 olur.
Yani R = 12 / 2 = 6 birimdir.
Çevrel Çemberin Yarıçapını Bulmanın Pratik Yolu
Bir üçgenin çevrel çemberinin yarıçapını bulmanın başka bir pratik yolu, üçgenin alanını kullanmaktır. Üçgenin alanı (A) ve kenar uzunlukları (a, b, c) ile yarıçap R arasında ilişki şudur:
R = (abc) / (4A)
Bu formülü kullanarak, üçgenin alanını ve kenar uzunluklarını bilerek R’yi hesaplayabilirsiniz. Alanı Heron Formülü ile bulabilirsiniz.
Umarım bu açıklamalar yardımcı olmuştur!