Sinüs Değerleri Kaçtır?
Sinüs değerleri, trigonometri alanında bir açının karşısındaki dik kenarın hipotenüse oranını ifade eder. Matematiksel hesaplamalarda önemli bir yere sahip olan sinüs fonksiyonu, -1 ile 1 arasında değişen değerler alır ve periyodik bir özellik gösterir. Uygulama alanları arasında fizik, mühendislik ve grafik tasarım bulunur.
Sinüs Değerleri Nedir?Sinüs değerleri, trigonometri alanında, bir açının karşısındaki dik kenarın hipotenüse oranını ifade eden matematiksel kavramlardır. Sinüs, genellikle "sin" sembolü ile gösterilir ve açıyla ilgili birçok hesaplamada önemli bir yer tutar. Sinüs fonksiyonu, bir açının ölçüsüne bağlı olarak değişen bir değer alır ve bu değer, -1 ile 1 arasında bir aralıkta bulunur. Sinüs Fonksiyonunun Matematiksel Tanımı Sinüs fonksiyonu, bir dik üçgenin geometrisi üzerinden tanımlanabilir. Aşağıdaki formül, sinüs değerlerini hesaplamak için kullanılır:
Burada θ, açıyı temsil eder. Örneğin, bir dik üçgende 30° açısının karşısındaki kenarın uzunluğu 1 birim ve hipotenüsün uzunluğu 2 birimse, sin(30°) = 1/2 = 0.5 olur. Sinüs Fonksiyonunun Özellikleri Sinüs fonksiyonunun bazı önemli özellikleri şunlardır:
Sinüs Değerlerinin Hesaplanması Sinüs değerleri, genellikle açı ölçüleri verilerek hesaplanır. Temel açıların sinüs değerleri şu şekildedir:
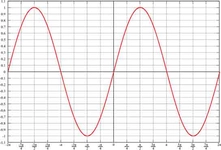
Bu değerler, trigonometrik tablolar veya hesap makineleri kullanılarak da bulunabilir. Ayrıca, sinüs değerleri, birim çember kullanılarak da gösterilebilir. Birim çemberde, açının ölçüsü, çemberin orijinal noktasından başlayarak saat yönünün tersine doğru ölçülür ve sinüs değeri, bu açının karşısındaki noktanın y koordinatına eşittir. Sinüs Değerlerinin Uygulamaları Sinüs değerleri, birçok farklı alanda kullanılmaktadır. Öne çıkan bazı uygulama alanları şunlardır:
Sonuç Sinüs değerleri, trigonometri alanında temel bir kavramdır ve çeşitli matematiksel hesaplamalara olan katkıları nedeniyle önemli bir yere sahiptir. Sinüs fonksiyonu, yalnızca matematiksel teorilerde değil, aynı zamanda mühendislik, fizik ve grafik tasarım gibi birçok pratik alanda da geniş bir kullanım alanı bulur. Bu nedenle, sinüs değerlerinin anlaşılması ve uygulanması, birçok bilim dalı için kritik bir öneme sahiptir. Ek Bilgiler Sinüs fonksiyonu ile ilgili daha ileri düzey konular arasında sinüs ve kosinüs ilişkisi, trigonometrik denklemler ve sinüs değerlerinin grafiksel temsili bulunmaktadır. Ayrıca, sinüs değerlerinin hesaplanmasında kullanılan çeşitli yöntemler arasında Taylor serileri ve Fourier analizi gibi matematiksel yaklaşımlar da yer almaktadır. Bu yöntemler, daha karmaşık matematiksel problemleri çözmede yardımcı olur. |













Matematik dersinde sinüs teoremini işlerken, a/sinA = b/sinB = c/sinC = 2r formülünü kullanarak bir örnek çözer misiniz? Özellikle çevrel çemberin yarıçapını nasıl bulacağımızı anlamakta zorlanıyorum.
Benay hanım, elbette size bir örnek çözebilirim.
Öncelikle, sinüs teoremi ile ilgili temel formülü hatırlayalım: a/sinA = b/sinB = c/sinC = 2r. Bu formül, bir üçgende kenarların sinüsleri ile olan oranlarının çevrel çemberin çapının iki katına eşit olduğunu ifade eder.
Örneğin, bir ABC üçgeninde a = 8, b = 6 ve A açısı 30° olsun. Çevrel çemberin yarıçapını (r) bulmak için:
1. İlk olarak, sinA'yı hesaplayalım:
sinA = sin(30°) = 1/2.
2. Sinüs teoremine göre:
a/sinA = 2r formülünden yararlanabiliriz.
3. Verilen değerleri yerine koyarsak:
8 / (1/2) = 2r olur.
4. Bu ifadeyi sadeleştirirsek:
8 2 = 2r.
5. Son olarak, 2r = 16 olduğundan:
r = 16 / 2 = 8.
Bu durumda, çevrel çemberin yarıçapı 8 birimdir. Umarım bu örnek, sinüs teoremini ve çevrel çemberin yarıçapını nasıl bulacağınızı anlamanıza yardımcı olur. Eğer başka sorularınız varsa, lütfen sormaktan çekinmeyin.