Sinüs Fonksiyonu ve Sinüs Teoremi Sinüs fonksiyonu, trigonometrinin temel taşlarından biridir ve matematikte birçok alanda kullanılır. Sinüs fonksiyonu, bir açının karşısındaki dik kenarın uzunluğunun hipotenüse oranı olarak tanımlanır. Matematiksel olarak, bir A açısının sinüsü "sin A" şeklinde gösterilir. Sinüs, kısaca "sin" olarak kısaltılır ve trigonometrik hesaplamalarda geniş bir kullanım alanı bulur. Sinüs Fonksiyonunun Tarihi Matematiğin tarihi, yazılı belgelere dayalı olarak yaklaşık 4500 yıl öncesine kadar uzanır. Bu uzun süreçte matematik, beş ana döneme ayrılarak incelenmiştir. İlk dönem, M.Ö. 6. yüzyıla kadar olan dönemi kapsar ve Mısır'da yapılan matematik çalışmalarını içerir. Mısır'da bilinen matematik, tam ve kesirli sayıların dört işlemi ile bazı geometrik şekillerin alan ve hacim hesaplarını kapsar. Sinüs Teoremi Sinüs teoremi, bir üçgendeki açılar ve kenarlar arasındaki ilişkileri belirlemek için kullanılan önemli bir teoremdir. Dik olmayan bir üçgende iki açıdan ve o açılardan birinin karşısındaki kenardan veya iki kenardan ve o kenarın karşısındaki açıdan bilinmeyen diğer açı ve kenarlar bu teorem sayesinde bulunabilir. Sinüs teoremi, şu şekilde ifade edilir:
Bu üç oran birbirine eşittir: a / sin(A) = b / sin(B) = c / sin(C) Sinüs Teoreminin Uygulaması Örneğin, a = 12, sin(A) = 0.98 ve sin(B) = 0.64 olsun. Bu durumda B kenarının uzunluğunu bulmak için: 12 / 0.98 = b / 0.64 12.24 = b / 0.64 b = 7.84 olarak bulunur. Sonuç Sinüs teoremi, üçgenlerin bilinmeyen kenar ve açılarını bulmada son derece yararlı ve kullanışlı bir teoremdir. Trigonometri, matematiğin bu ve benzeri teoremlerle zenginleşmiş bir dalıdır ve birçok bilimsel ve mühendislik alanında geniş uygulama alanı bulur. |
Jeyn
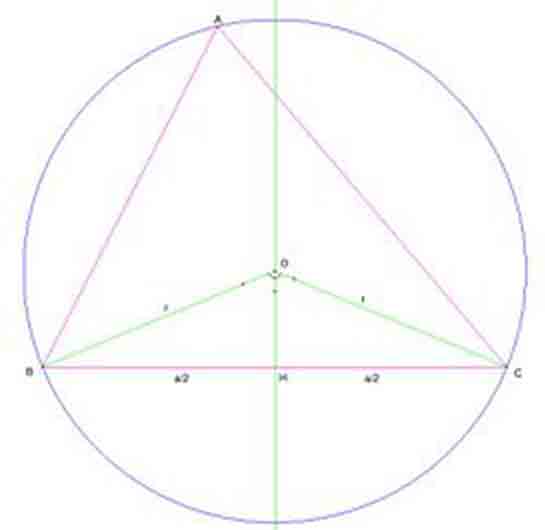
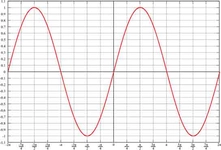
24 Temmuz 2024 ÇarşambaSinüs fonksiyonu ve sinüs teoremi üzerine çalışırken, trigonometrinin bu temel taşlarının gerçekten birçok alanda kullanıldığını gördüm. Peki, bir üçgendeki bilinmeyen açı ve kenarları bu teorem sayesinde bulmak neden bu kadar önemli? Sinüs fonksiyonunun tarihsel gelişimi hakkında daha fazla bilgi nereden bulabilirim?
Cevap yazAdmin
24 Temmuz 2024 ÇarşambaMerhaba Jeyn,
Trigonometrinin temel taşları olan sinüs fonksiyonu ve sinüs teoremi, birçok alanda kritik öneme sahiptir. Bir üçgendeki bilinmeyen açı ve kenarları bulmak, mühendislikten astronomiye, fizikten bilgisayar grafiklerine kadar geniş bir yelpazede uygulama alanı bulur. Örneğin, mühendisler köprü ve bina tasarımlarında bu teoremleri kullanarak doğru hesaplamalar yapar. Astronomlar ise gök cisimlerinin konumlarını belirlemede bu matematiksel araçlardan yararlanır.
Sinüs fonksiyonunun tarihsel gelişimi hakkında daha fazla bilgi edinmek için, matematik tarihi üzerine yazılmış kitapları ve akademik makaleleri inceleyebilirsin. Özellikle, antik Yunan, Hint ve İslam matematikçilerinin trigonometrik fonksiyonların temellerini nasıl attıkları konusunda zengin kaynaklar mevcuttur. Ayrıca, çevrimiçi eğitim platformlarında ve üniversite kütüphanelerinde bu konulara dair kapsamlı ders notları ve videolar bulabilirsin.
Umarım bu bilgiler senin için faydalı olmuştur, iyi çalışmalar!